Welcome to Bindog's Blog!
追求技术 永无止境-
训练时显存优化技术——OP合并与gradient checkpoint
背景
前几天看到知乎上的文章FLOPs与模型推理速度,文中提到一个比较耗时又占显存的pointwise操作
x * sigmoid(x),这实际上是swish activation;暂且不提它背后的争议,本文主要想从这个结构入手来优化它的显存占用以及耗时,并讨论更广泛的训练时显存优化技术。反向传播是如何工作的?
要分析清楚swish activation为什么会比较占显存,我们首先需要搞清楚反向传播是如何工作的,或者更进一步说,现有的自动求导框架是如何求出梯度的。
先明确一点,所谓自动求导框架实际上是“半自动”的:它并非直接求出一个复杂函数导数的解析形式,而是通过构建计算图和预先写好的基础函数的求导规则,结合链式求导法则实现的自动求导。
以swish acivation为例进行说明,其表达式为
f(x) = x * sigmoid(x),通过简单的数学推导得到其梯度的解析式为f'(x) = sigmoid(x) + x * sigmoid(x) * (1 - sigmoid(x));先把这个结果放一边,看看自动求导框架是如何一步步求出这个结果的,画出计算图如下:
除了计算图以外,我们还需要定义几个基本函数的求导规则,在这个例子里涉及两个函数,一个是乘法,另一个是sigmoid函数(实际上sigmoid也是由几个基本函数构成的,这里我们将其视为一个整体)
f(x, y) = x * y # gradient for x: y # gradient for y: x g(x) = sigmoid(x) # 1 / (1 + exp(-x)) # gradient for x: sigmoid(x) * (1 - sigmoid(x))回到刚才的计算图上,反向传播先经过乘法运算,根据上面的求导规则,路径1上的梯度为
sigmoid(x),路径3上的梯度为x;路径3再反向传播要经过路径2,除了sigmoid(x)本身的梯度外,还要乘上输入进来的梯度x,所以最终路径2上的梯度为x * sigmoid(x) * (1 - sigmoid(x)),路径2和路径1汇聚到一起,所以最终的梯度为sigmoid(x) + x * sigmoid(x) * (1 - sigmoid(x)),刚好等于我们用数学公式计算出来的结果。自动求导框架正是依靠这些基础的规则和链式求导法则在高效准确的运作。显存被谁吃掉了
先说一个结论,在绝大多数神经网络的训练过程中,显存占用的大头是中间结果,也就是所谓的“特征图”。那我们为什么要保留中间结果呢?当然是为了方便求导啊!还是以swish acivation为例,把它放入神经网络来看,x就是前一层输出的中间结果(特征图)
-
在适用乘法的求导规则时,要求我们要事先保留下中间结果x和sigmoid(x),有人可能会说只保留一个x不就可以了吗?sigmoid(x)可以通过计算得出,注意框架定义的乘法及其求导规则是通用规则,乘法的左右两边完全可能是不相关的两个值,所以必须同时保留下来。
-
在对sigmoid函数适用求导规则时,需要存下中间结果x。
在不考虑框架自身优化的情况下,显存占用就包括了两个x和一个sigmoid(x),注意x可不是一个单独的数值,而是类似
32x32x128这样大小的特征图,考虑到swish acivation在网络中数量庞大,每出现一次就意味着巨大的显存浪费。手动合并OP
那么有没有办法优化呢?当然是可以的,既然我们能用数学公式提前算出swish acivation的梯度,那么直接将其视为一个整体不就好了?无非就是定义一个新的函数和新的求导规则
swish(x) = x * sigmoid(x) # gradient for x: sigmoid(x) + x * sigmoid(x) * (1 - sigmoid(x))这样一来,计算图变成了下面这个样子:

x的梯度可以直接根据新的规则求出,而在新的规则下,我们只需要保留x这一个中间结果即可,sigmoid(x)可以根据x求出。
所以说,自动求导框架虽然省事,但是其缺陷也很明显,由于大部分求导规则是面向通用的函数,很难针对特定的场景进行自动优化而导致显存浪费。对swish acivation这样的函数,只能依靠工程师的经验手动的进行优化。
需要指出的是,现有的一些框架如TVM和TensorRT也能自动的对某些算子进行融合,进而大大提高计算效率,降低显存消耗,但是这些都属于部署阶段了,而本文讨论的均为训练阶段。
类似的优化案例还有inplace-abn,针对的是类似
BN-ReLU-Conv这样的常见结构组合,如下所示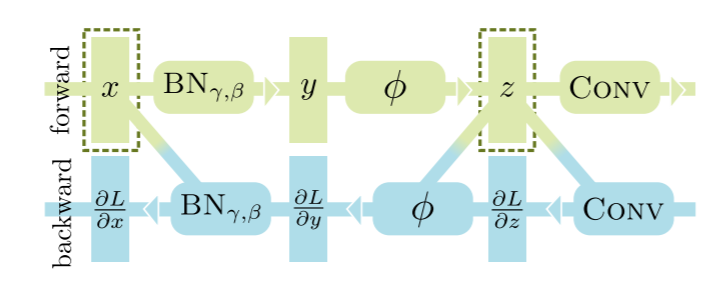
图中的虚线框是需要保留的中间结果,inplace-abn的优化思路是只保留中间结果
z,通过反推得到x,然而众所周知ReLU是不可逆的运算,因此inplace-abn将其替换为了Leaky ReLU,计算图变成了如下形式: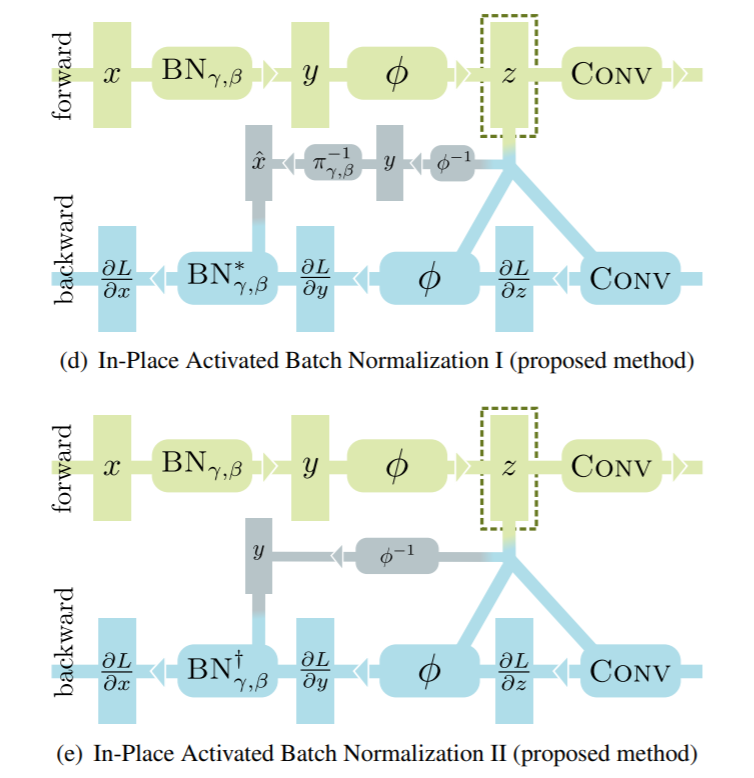
接下来的事情就是用数学的方式手动求出导数,然后定义成规则即可。
对I型,我们有
\[\begin{array}{c} \frac{\partial y_{j}}{\partial \gamma}=\hat{x}_{j}, \quad \frac{\partial y_{j}}{\partial \beta}=1, \quad \frac{\partial y_{j}}{\partial \hat{x}_{j}}=\gamma \\ \frac{\partial L}{\partial \gamma}=\sum_{j=1}^{m} \frac{\partial L}{\partial y_{j}} \frac{\partial y_{j}}{\partial \gamma}=\sum_{j=1}^{m} \frac{\partial L}{\partial y_{j}} \hat{x}_{j}, \quad \frac{\partial L}{\partial \beta}=\sum_{j=1}^{m} \frac{\partial L}{\partial y_{j}} \frac{\partial y_{j}}{\partial \beta}=\sum_{j=1}^{m} \frac{\partial L}{\partial y_{j}}, \quad \frac{\partial L}{\partial \hat{x}_{j}}=\frac{\partial L}{\partial y_{j}} \frac{\partial y_{j}}{\partial \hat{x}_{j}}=\frac{\partial L}{\partial y_{j}} \gamma \\ \frac{\partial \hat{x}_{j}}{\partial \sigma_{\mathcal{B}}^{2}}=-\frac{1}{2\left(\sigma_{\mathcal{B}}^{2}+\epsilon\right)} \frac{x_{j}-\mu_{\mathcal{B}}}{\sqrt{\sigma_{\mathcal{B}}^{2}+\epsilon}}=-\frac{\hat{x}_{j}}{2\left(\sigma_{\mathcal{B}}^{2}+\epsilon\right)}, \quad \frac{\partial \hat{x}_{j}}{\partial \mu_{\mathcal{B}}}=-\frac{1}{\sqrt{\sigma_{\mathcal{B}}^{2}+\epsilon}} \\ \frac{\partial L}{\partial \sigma_{\mathcal{B}}^{2}}=\sum_{j=1}^{m} \frac{\partial L}{\partial \hat{x}_{j}} \frac{\partial \hat{x}_{j}}{\partial \sigma_{\mathcal{B}}^{2}}=-\frac{\gamma}{2\left(\sigma_{\mathcal{B}}^{2}+\epsilon\right)} \sum_{j=1}^{m} \frac{\partial L}{\partial y_{j}} \hat{x}_{j}=-\frac{\gamma}{2\left(\sigma_{\mathcal{B}}^{2}+\epsilon\right)} \frac{\partial L}{\partial \gamma} \\ \frac{\partial L}{\partial \mu_{\mathcal{B}}}=\sum_{j=1}^{m} \frac{\partial L}{\partial \hat{x}_{j}} \frac{\partial \hat{x}_{j}}{\partial \mu_{\mathcal{B}}}=-\frac{\gamma}{\sqrt{\sigma_{\mathcal{B}}^{2}+\epsilon}} \sum_{j=1}^{m} \frac{\partial L}{\partial y_{j}}=-\frac{\gamma}{\sqrt{\sigma_{\mathcal{B}}^{2}+\epsilon}} \frac{\partial L}{\partial \beta} \\ \frac{\partial \sigma_{\mathcal{B}}^{2}}{\partial x_{i}}=\frac{2\left(x_{i}-\mu_{\mathcal{B}}\right)}{m}, \quad \frac{\partial \mu_{\mathcal{B}}}{\partial x_{i}}=\frac{1}{m}, \quad \frac{\partial \hat{x}_{i}}{\partial x_{i}}=\frac{1}{\sqrt{\sigma_{\mathcal{B}}^{2}+\epsilon}} \\ \frac{\partial L}{\partial x_{i}}=\frac{\partial L}{\partial \hat{x}_{i}} \frac{\partial \hat{x}_{i}}{\partial x_{i}}+\frac{\partial L}{\partial \sigma_{\mathcal{B}}^{2}} \frac{\partial \sigma_{\mathcal{B}}^{2}}{\partial x_{i}}+\frac{\partial L}{\partial \mu_{\mathcal{B}}} \frac{\partial \mu_{\mathcal{B}}}{\partial x_{i}}=\left(\frac{\partial L}{\partial y_{i}}-\frac{1}{m} \frac{\partial L}{\partial \gamma} \hat{x}_{i}-\frac{1}{m} \frac{\partial L}{\partial \beta}\right) \frac{\gamma}{\sqrt{\sigma_{\mathcal{B}}^{2}+\epsilon}} \end{array}\]对II型,更进一步,直接用$y_i=\hat x_i * \gamma + \beta$的反函数,$\hat x_i=\frac{y_i-\beta}{\gamma}$进行替换即可
\[\begin{array}{c} \frac{\partial L}{\partial \gamma}=\sum_{j=1}^{m} \frac{\partial L}{\partial y_{j}} \hat{x}_{j}=\sum_{j=1}^{m} \frac{\partial L}{\partial y_{j}} \frac{y_{j}-\beta}{\gamma}=\frac{1}{\gamma} \sum_{j=1}^{m} \frac{\partial L}{\partial y_{j}} y_{j}-\frac{\beta}{\gamma} \sum_{j=1}^{m} \frac{\partial L}{\partial y_{j}}=\frac{1}{\gamma}\left[\sum_{j=1}^{m} \frac{\partial L}{\partial y_{j}} y_{j}-\beta \frac{\partial L}{\partial \beta}\right] \\ \frac{\partial L}{\partial x_{i}}=\left(\frac{\partial L}{\partial y_{i}}-\frac{1}{m} \frac{\partial L}{\partial \gamma} \hat{x}_{i}-\frac{1}{m} \frac{\partial L}{\partial \beta}\right) \frac{\gamma}{\sqrt{\sigma_{\mathcal{B}}^{2}+\epsilon}} \\ =\left(\frac{\partial L}{\partial y_{i}}-\frac{1}{m} \frac{\partial L}{\partial \gamma} \frac{y_{i}-\beta}{\gamma}-\frac{1}{m} \frac{\partial L}{\partial \beta}\right) \frac{\gamma}{\sqrt{\sigma_{\mathcal{B}}^{2}+\epsilon}} \\ =\left[\frac{\partial L}{\partial y_{i}}-\frac{1}{\gamma m} \frac{\partial L}{\partial \gamma} y_{i}-\frac{1}{m}\left(\frac{\partial L}{\partial \beta}-\frac{\beta}{\gamma} \frac{\partial L}{\partial \gamma}\right)\right] \frac{\gamma}{\sqrt{\sigma_{\mathcal{B}}^{2}+\epsilon}} \end{array}\]虽然推导过程有些复杂,但写出求导公式后,我们只需要将其封装进手写的模块中即可。原论文中的实现表明,采用Inplace-abn后,显存占用最高可下降50%左右,而且由于
Leaky ReLU实际效果其实与ReLU非常接近,省下来的显存可以用于提高batch_size,模型训练实际上能从中得到更大收益。还能更进一步吗?
回想前面的优化过程,我们发现其实这是一种典型的时间换空间的做法,虽然模型占用的显存下降了(舍弃了大量中间结果),但是我们定义的求导规则非常复杂,计算步骤明显多于优化前,其根本原因并非是不需要中间结果,而是有办法在求导过程中实时的计算出之前被舍弃掉的中间结果。考虑GPU上显存资源与计算资源的关系,只用较少的计算量和额外的一点计算时间换取宝贵的显存资源,这么做实际上是划算的。
如果沿着这个思路更进一步,所有的中间结果都不需要存储了,只需要存最初的输入即可,因为所有的中间结果都可以由输入重新计算得到,然而这个方案显然是不划算的,因为反向传播的过程是“由深入浅”,而计算中间结果的过程是“由浅入深”,二者的方向并不匹配,每当我们需要中间结果时就需要从头再来一遍,这样的计算和时间开销显然是不划算的。
如果折中一下呢?这就是OpenAI提出的
gradient-checkpoint的思路,在神经网络中间设置若干个检查点(checkpoint),检查点以外的中间结果全部舍弃,反向传播求导数的时间,需要某个中间结果时,从最近的检查点开始计算,这样既节省了显存,又避免了从头计算的繁琐过程;从代码层面来看,原版实现用的是tensorflow,由于是静态图的缘故,需要用到grapheditor等一系列骚操作,而且包含了很多“智能”寻找bottleneck选择为checkpoint的代码,很容易劝退新人。但是如果看一下pytorch的官方实现,你会惊讶的发现
gradient-checkpoint的核心部分出奇的简单,这也算是动态图以及pytorch的一点小优势吧,当然pytorch版本的实现并不包括智能寻找checkpoint点的功能,需要人为设定。核心代码如下所示:class CheckpointFunction(torch.autograd.Function): @staticmethod def forward(ctx, run_function, preserve_rng_state, *args): check_backward_validity(args) ctx.run_function = run_function ctx.preserve_rng_state = preserve_rng_state if preserve_rng_state: ctx.fwd_cpu_state = torch.get_rng_state() # Don't eagerly initialize the cuda context by accident. # (If the user intends that the context is initialized later, within their # run_function, we SHOULD actually stash the cuda state here. Unfortunately, # we have no way to anticipate this will happen before we run the function.) ctx.had_cuda_in_fwd = False if torch.cuda._initialized: ctx.had_cuda_in_fwd = True ctx.fwd_gpu_devices, ctx.fwd_gpu_states = get_device_states(*args) ctx.save_for_backward(*args) with torch.no_grad(): outputs = run_function(*args) return outputs @staticmethod def backward(ctx, *args): if not torch.autograd._is_checkpoint_valid(): raise RuntimeError("Checkpointing is not compatible with .grad(), please use .backward() if possible") inputs = ctx.saved_tensors # Stash the surrounding rng state, and mimic the state that was # present at this time during forward. Restore the surrounding state # when we're done. rng_devices = [] if ctx.preserve_rng_state and ctx.had_cuda_in_fwd: rng_devices = ctx.fwd_gpu_devices with torch.random.fork_rng(devices=rng_devices, enabled=ctx.preserve_rng_state): if ctx.preserve_rng_state: torch.set_rng_state(ctx.fwd_cpu_state) if ctx.had_cuda_in_fwd: set_device_states(ctx.fwd_gpu_devices, ctx.fwd_gpu_states) detached_inputs = detach_variable(inputs) with torch.enable_grad(): outputs = ctx.run_function(*detached_inputs) if isinstance(outputs, torch.Tensor): outputs = (outputs,) torch.autograd.backward(outputs, args) grads = tuple(inp.grad if isinstance(inp, torch.Tensor) else inp for inp in detached_inputs) return (None, None) + grads注意到最近旷视开源的MegEngine,在PR的时候提到一个亚线性显存优化技术,其实就是
gradient-checkpoint技术,详情可参考论文Training Deep Nets with Sublinear Memory Cost,当然MegEngine肯定在细节上对其进行了一些优化,本文就不展开讨论了。CUDA版的swish activation
回到swish activation的优化上来,如果要追求效率的极致提升,下一步考虑的方案应该是手写C++ extension,将计算从python层面转移到C++与CUDA上。
如何基于 pytorch写C++扩展,官方文档上有非常详细的教程,写法和方式也都比较灵活,可以根据自己的习惯进行选择,这里我们选择利用setuptools的方式进行构建
pytorch在用户自定义扩展上也是做了非常多的支持,用户能非常方便的使用pytorch底层定义好的一些类和函数;在写CUDA函数时,pytorch还提供了一个
CUDAApplyUtils.cuh头文件,专门用于优化pointwise操作的情况,以减小拷贝和临时存储的显存浪费(用于lambda函数,函数名非常直观,CUDA_tensor_applyN表示操作数的个数,N可以为1,2,3,4,用户还可以指定每个操作数的属性,如只读/读写,针对每对情形都有专门的优化实现)对于swish activation来说,由于全是pointwise操作,利用这个优化技巧可以把显存占用进一步压缩。具体代码可参考swish_optimize
简单对比一下以上几种实现在实际场景中(单卡RTX 2070,resnet50, bs=32)的显存占用情况和运行时间(一次forward & 一次backward & 参数更新)
- 无优化纯Python:GPU memory=6383MB,time=223ms
- 合并算子(Python):GPU memory=5139MB,time=234ms
- 合并算子(CUDA):GPU memory=5143MB,time=188ms
从上述对比结果来看,结果基本符合前文的分析,纯Python的实现下,显存优化后的由于是时间换空间,所以显存占用降低了,而时间稍有增加;在CUDA版本的优化下,一方面得益于C++的高效,另一方面得益于由于pointwise计算的优化,在显存占用降低的同时,计算时间也大幅缩短
如果觉得本文对您有帮助,欢迎打赏我一杯奶茶钱~

-
-
混合精度训练与模型并行适配
背景
混合精度训练出现了有好几年的时间了,由于前东家的卡是老古董的GTX 1080 Ti,不支持FP16,一直没有时间真正用起来。刚好最近有朋友反馈混合精度训练在之前的模型并行上有点问题,所以跟进研究了一下
当然,本文不仅是修复了一些小问题,同时也分析了混合精度训练中所使用的一些技巧原理
混合精度训练
如果训练使用的框架是pytorch,那么首选的应该是N厂的apex,经过好几年的迭代,目前的apex使用起来已经非常傻瓜,基本上能用的trick全都已经集成了,看一遍
README里面的示例就知道怎么改造自己的程序了。刚才提到混合精度训练中的trick,这篇论文是必读文献,里面囊括了几个非常重要的trick:FP32 master copy of weights和loss scaling等
其实本质都是一样的:因为半精度的数值表示范围比单精度要小很多,所以需要从各个方面来减小累积误差(FP32 master copy of weights),充分利用FP16的表示范围(loss scaling),必要时使用FP32来进行计算(尤其是一些极其容易溢出计算如exp)
-
FP32 master copy of weights,这个方法起因是大数加小数会引起的误差,我们知道浮点数在计算机中的表示是指数和尾数的形式,在计算过程中包含对阶、尾数运算、规格化、舍入处理、溢出判断几个步骤,而在对阶过程中,若两数相差较大,很容易产生误差。FP32的表示范围较宽,而FP16表示范围较小,因此有一些在FP32表示范围下不会出现问题的加减运算,在FP16下就会出现误差,由此诞生了这样一个方法:即在前向传播和反向传播过程中,使用的均为FP16,而在
optimizer.step()这一步中,将梯度转换为FP32,并与FP32 master copy of weight做运算更新权重,下一次前向计算时,再从FP32 master copy of weight中取值转换为FP16计算,重复上述过程。图示如下: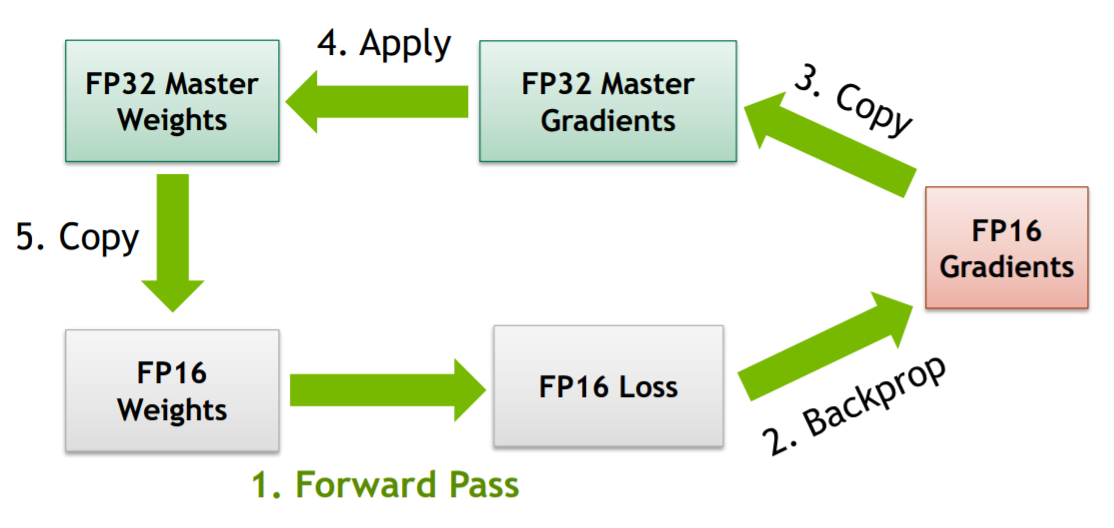
-
loss scaling,这个方法是通过统计得出来的,据论文作者观察,大量梯度的值集中在如下的这个区间内,几乎浪费了FP16一半以上的表示范围,同时有大量值出现了下溢的情况,直接变为0。
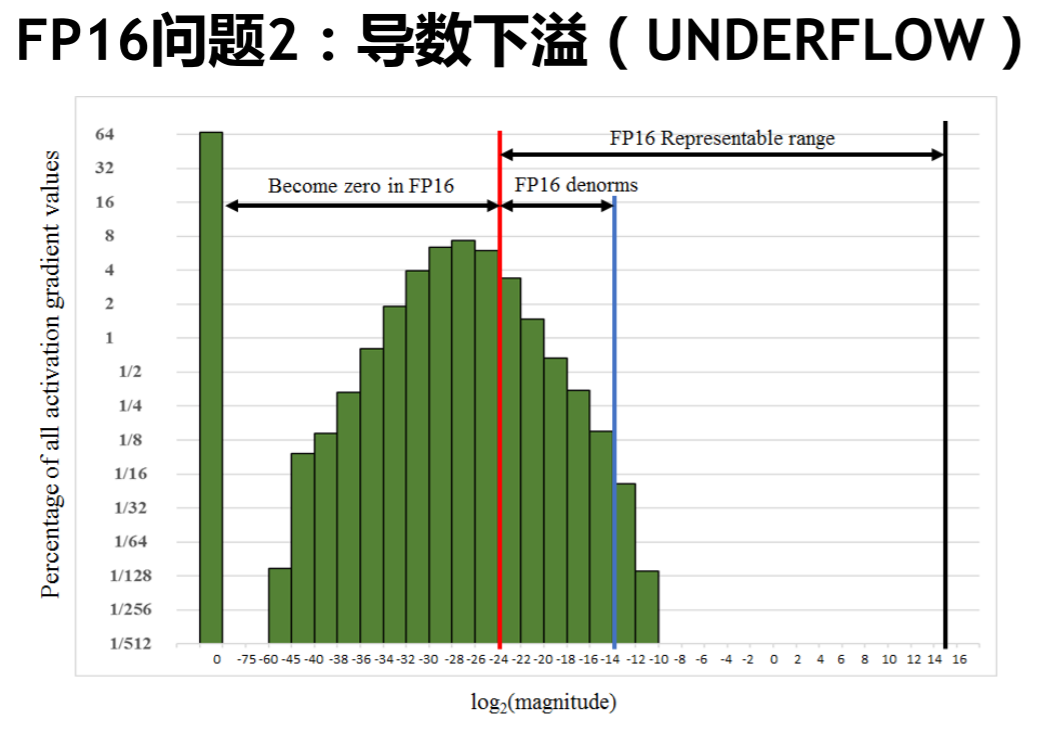
所以有必要人为的对梯度进行放大,充分利用FP16的表示空间,这正是loss scaling的目的,对最终的loss乘以一定的scale(可设置为一个常数,可根据实际情况统计得出,也可动态调整),根据链式求导法则,我们实际上对计算链路中所有的梯度均做了放大。接下的步骤就是与第一个方法相结合,将scale后的FP16梯度复制成FP32再做unscale,最后与FP32 master copy of weights累加即可。整个过程如下所示:
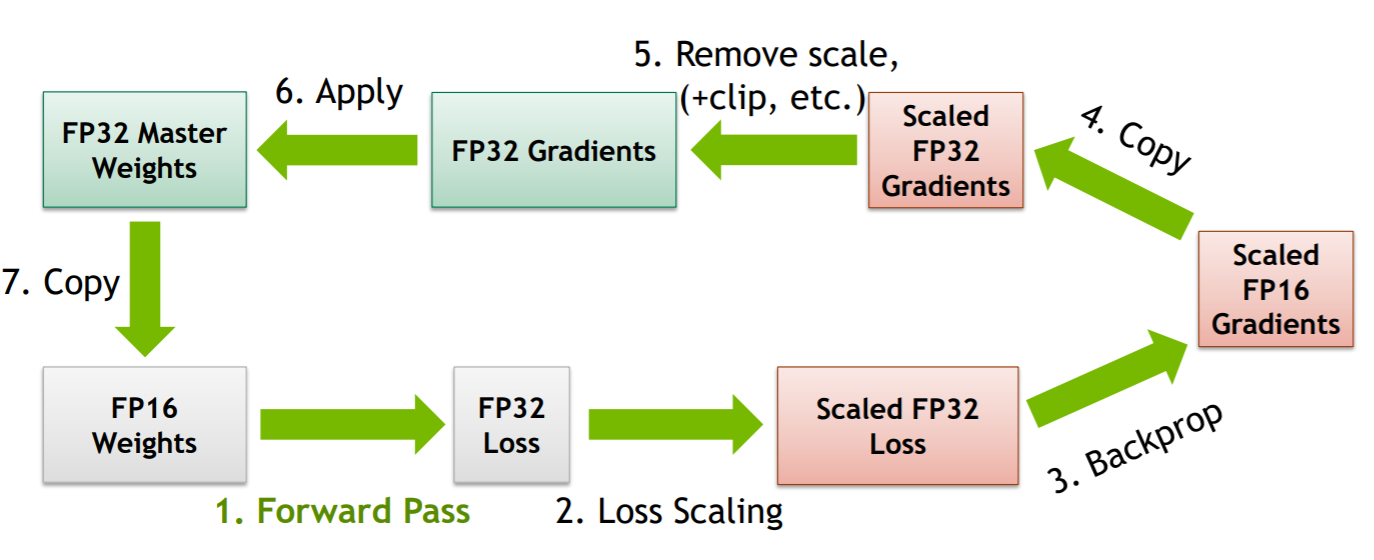
上述内容是对于底层实现原理层面的解释,在使用上apex封装的非常傻瓜了,使用样例如下所示:
# Initialization opt_level = 'O1' model, optimizer = amp.initialize(model, optimizer, opt_level=opt_level) # Train your model ... with amp.scale_loss(loss, optimizer) as scaled_loss: scaled_loss.backward() ...正常情况下,如果定义的模型没有引入一些第三方外部模块,都是常见的一些网络的话,那么使用起来是没有什么总是的。但如果使用了一些外部模块(CUDA实现的一些新算子等)不支持FP16,那么我们需要对相应的函数做一些标记注册
@amp.float_function,典型的例子如这个DCN实现至此,基本的混合精度训练就介绍完了,下面聊聊在改造模型并行程序适配混合精度训练中遇到的一些问题。
模型并行改造
对之前模型并行不熟悉的同学可参考这篇文章:如何支撑上亿类别的人脸训练?——显存均衡的模型并行(PyTorch实现)
改造过程主要涉及三部分,一是由于pytorch在1.3.0版本后仅支持
@staticmethod形式的torch.autograd.Function,所以需要对之前所写的ModelParallelCrossEntropy进行重写,二是由于ModelParallelCrossEntropy所处的位置非常尴尬,它不属于深度学习网络的一部分,也不包括任何参数,是最后计算loss的模块,因此有些操作不能靠apex自动完成,需要手动加上;三是一个细节优化,在原来的实现中,one-hot label也是一个显存消耗大户,尤其是label数量到达百万级别后,这里我们使用sparse tensor对其进行优化。重写@staticmethod
pytorch官方文档中有专门的一篇教程说明如何自定义一个新的
Function,注意和原来实现的主要区别在于:- 没有了初始化函数__init__
- forward和backward函数均为
@staticmethod - forward和backward函数中原来的
self由ctx替代,功能类似
注意,由于没有了初始化函数,我们无法在初始化的时候传入一些控制参数,如显卡数量、是否计算loss等,只能在forward的时候将其传入(forward只接受tensor类型参数,布尔型等参数需要根据情况进行转换),在backward的时候,对这些参数我们也需要返回其梯度(None即可)
backward中的问题修复
文章开始说的模型并行的问题主要是由于scale_loss引起的(如果不使用scale_loss是可以正常收敛的,但是最终效果会差一些),根据前面的原理讲解我们知道:scale_loss是通过链式求导法则将最后乘在loss上的scale反向传播到整个网络中的梯度中去的,而我之前那个版本实现的backward是有问题的,假定了loss是整个计算图的最后一个操作,并未考虑到scale这种情况,导致整个网络中的梯度并没有被放大,训练也就无法进行下去(非常羞愧……);解决过程并不复杂,核心在于理解backward的机制和参数含义,在之前的那篇文章中提到过,forward的返回值要与backward的参数一一对应,forward的参数要与backward的返回值一一对应,如下图所示:
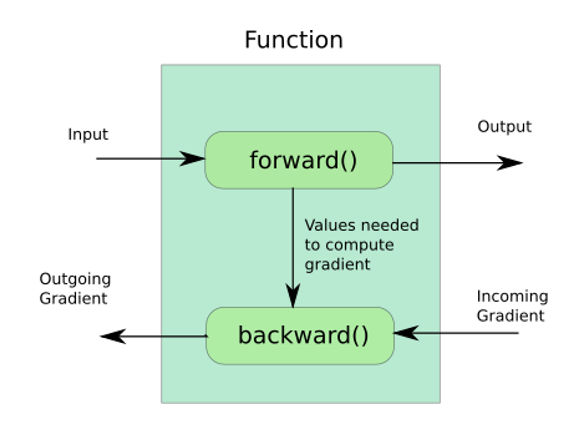
那么在
ModelParallelCrossEntropy这个Function中,我们之前忽略掉的backward的输入参数loss_grad到底是什么?结合前面的描述和配图,仔细思考一下就清楚了:forward时最终输出的是loss,而在混合精度训练情况下后面还有一步,即scaled_loss=loss*scale,那么backward时,loss_grad=d(scaled_loss)/d(loss)=scale;所以在计算完梯度后,根据链式求导法则,我们需要把原梯度乘上scale才能保证结果的正确性,修复了这里在混合精度下即可正常收敛了。这里再提一句,backward本身支持一个grad_tensors参数,相当于人为的传进去一个梯度,在某些特殊的情况下是有用的,例如forward输出的值为一个向量Tensor,更多细节可参考这篇知乎专栏
使用sparse tensor
原先在生成one-hot label tensors时,参考的是pytorch官方论坛上的一个实现,当时并未多想,实际情况若label数量到达百万级别,one-hot label也是一个显存消耗大户,因此考虑使用sparse tensor对其进行改造。然而由于
torch.sparse仍然不成熟,许多操作如scatter并不支持,所以需要我们手工的去做分片操作,这就纯属体力活了不用细讲了,直接看代码即可总结
本次改进的更新仍在原来的repo
apex_debug分支下,后续有更好的思路我也会持续更新,也欢迎大家提issue如果觉得本文对您有帮助,欢迎打赏我一杯奶茶钱~

参考文献
-
-
深度学习模型转换与部署那些事(含ONNX格式详细分析)
背景
深度学习模型在训练完成之后,部署并应用在生产环境的这一步至关重要,毕竟训练出来的模型不能只接受一些公开数据集和榜单的检验,还需要在真正的业务场景下创造价值,不能只是为了PR而躺在实验机器上
在现有条件下,一般涉及到模型的部署就要涉及到模型的转换,而转换的过程也是随着对应平台的不同而不同,一般工程师接触到的平台分为GPU云平台、手机和其他嵌入式设备
对于GPU云平台来说,在上面部署本应该是最轻松的事情,但是实际情况往往比较复杂。有历史遗留问题,比如说3年前的古董级的模型因为效率和推理速度问题需要进行优化,也有算法团队使用了一些比较小众或者自定义的OP的问题。其实解决这类问题有非常直接的方式,例如直接用最新的框架重新训练,或者算法团队对模型做一些妥协,替换掉一些骚操作,那么对部署工程师来说问题就简单了很多。但是有些情况下(算法团队很忙或者必须效果优先),我们只能自己从框架的层面来解决这个问题,包括但不限于:实现新OP、修改不兼容的属性、修改不兼容的权重形状
-
为什么triplet loss有效?
0x00 triplet loss简介
深度学习领域有一块非常重要的方向称之为metric learning,其中一个具有代表性的方法就是triplet loss,triplet loss的基本思想很清晰,就是让同一类别样本的feature embedding尽可能靠近,而不同类别样本的feature embedding尽可能远离,其中样本的feature embedding是通过同一个深度神经网络抽取得到的。
-
如何支撑上亿类别的人脸训练?——显存均衡的模型并行(PyTorch实现)
去年的工作了,一直没抽出时间整理出来,模型并行看似神秘,在网上搜索相关资料的时候大部也是以谈原理的居多,唯独少了有人拿出代码来捅破这层窗户纸。这里我放出一个PyTorch版本的Demo供大家参考交流。
-
Kaldi内存泄漏问题排查
最近在做Kaldi相关开发的过程中,遇到了一个非常棘手的内存问题,现将整个排查解决过程梳理一下,希望对有类似问题的同学有帮助。
0x00 情况概述
Kaldi是一个语音识别的C++开发框架,集成了非常多的工具和模块。由于项目需要,希望能够将CVTE开源的模型部署到内部线上测试使用,且能够充分利用GPU加速,而网上的教程大多都是基于
offline模式,使用的是nnet3和nnet3bin下面的模块和程序。