0x00 triplet loss简介
深度学习领域有一块非常重要的方向称之为metric learning,其中一个具有代表性的方法就是triplet loss,triplet loss的基本思想很清晰,就是让同一类别样本的feature embedding尽可能靠近,而不同类别样本的feature embedding尽可能远离,其中样本的feature embedding是通过同一个深度神经网络抽取得到的。
在triplet loss中,我们会选取一个三元组,首先从训练集中选取一个样本作为Anchor,然后再随机选取一个与Anchor属于同一类别的样本作为Positive,最后再从其他类别随机选取一个作为Negative,这里将样本的feature embedding记为$x$,那么一个基本的三元组triplet loss如下:
\[l_{tri}=\max (\Vert x_a - x_p \Vert - \Vert x_a - x_n \Vert + \alpha, 0)\]其中$\alpha$为margin;上式要求Negative到Anchor的距离至少要比Positive到Anchor的距离大$\alpha$,显然$\alpha$越大不同类别之间的可区分性就越强,相应的训练难度也越大。当然也可以把$\alpha$设为0,这样条件就放的比较宽松了,但是triplet loss的优势也就很难体现出来了。
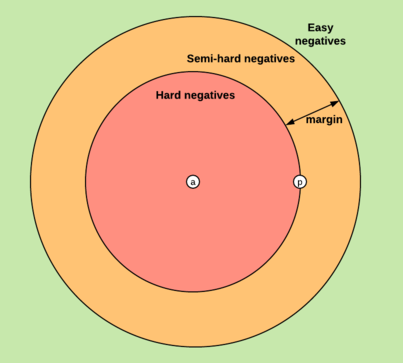
在triplet loss基础上,又衍生出了其他许多改进和变体,例如一个比较有效的方法叫hard mining,在三元组选择过程中加入一些特定的策略,尽量选择一些距离Anchor较远的Positive和距离Anchor较近的Negative(也就是最不像的同类样本、最像的不同类样本)……此类方法还有许多,就不一一列举了。
然而triplet loss虽然有效,但是其常为人诟病的缺点也很明显:训练过程不稳定,收敛慢,需要极大的耐心去调参……所以在很多情况下,我们不会单独使用triplet loss,而是将其与softmax loss等方法相结合使用,以稳定训练过程。
关于triplet loss的基本介绍就到这里,这不是本文的重点。本文关注的点是对triplet loss本质的探索,以及triplet loss和原来的softmax loss的关联,为什么它在不显示的引入label的情况下能够近似的达到分类的效果?最近在读到A Theoretically Sound Upper Bound on the Triplet Loss for Improving the Efficiency of Deep Distance Metric Learning这篇论文后,结合我们之前做的一些实践认知和经验,似乎有了更进一步的认识,这里会有一点涉及到理论层面的分析(也就是公式推导,但并不复杂)。总而言之我们会发现,triplet loss在某种意义上而言和我们用softmax loss并没有什么不同,只不过它对分类边界上的要求更为严格。
0x01 一点点理论分析
我们回到triplet loss当中三元组的基本形式,首先约定一些符号(与上面提到的那篇论文保持一致),假定训练集样本总量为$N$,定义同类别样本集合$S = \{(i,j) \mid y_i = y_j \}_{i,j\in \{1,\cdots N \}}$,那么最基本的triplet loss表达式形式如下(为了简化问题,我们暂时忽略了margin这一项)
\[L_t(T,S)=\sum\limits_{(i,j)\in S,(i,k)\notin S,i,j,k\in\{1,\cdots,N\}}l_t(x_i,x_j,x_k) \tag{1}\] \[l_t(x_i,x_j,x_k)=\Vert x_i-x_j \Vert - \Vert x_i - x_k \Vert \tag{2}\]直接对上面两个式子做变换是比较困难的,如果假定每一个类别都有自己的一个类中心$c_m$,当然这个类中心和所有的样本处于同一个embedding空间,$\mathcal{C}=\{c_m\}_{m=1}^C$,其中$c_m\in \mathbb{R}^D$
通过引入这样一个辅助的类中心点,我们可以利用三角不等式写出如下式子:
\[\Vert x_i-x_j \Vert \leq \Vert x_i-c_{y_i} \Vert + \Vert x_j-c_{y_i} \Vert \tag{3}\] \[\Vert x_i - x_k \Vert \geq \Vert x_i-c_{y_k} \Vert - \Vert x_k-c_{y_k} \Vert \tag{4}\]根据上面几个式子,我们可以写出$l_t(x_i,x_j,x_k)$的一个上界$l_d(x_i,x_j,x_k)$,如下
\[l_d(x_i,x_j,x_k)=\Vert x_i-c_{y_i} \Vert - \Vert x_i-c_{y_k} \Vert + \Vert x_j-c_{y_i} \Vert + \Vert x_k-c_{y_k} \Vert \tag{5}\]当然这只是其中一个三元组的loss,还不太容易观察出规律,如果考虑整个训练集上所有可能的三元组,累加得到整体的triplet loss就可以看出一些有意思的东西了。那么符合条件的三元组有多少个呢?为了简化分析流程,我们要做一个合理的假定,那就是训练集当中每个类别的样本数量是相等的(不相等的话可以通过采样的方式使之相等),通过简单的排列组合知识可以得出三元组的个数为$A_C^2 \cdot A_{\frac{N}{C}}^2 \cdot C_{\frac{N}{C}}^1$;然后我们仔细观察式(5)可以发现,它实际上是由两部分构成的,一部分是样本减去其对应的类中心,另一部分是样本减去其他类别的类中心。所以稍微整合一下即可得到整体的triplet loss,如下所示:
\[L_d(T,S)=G\sum\limits_{i=1}^N(\Vert x_i-c_{y_i} \Vert - \frac{1}{3(C-1)}\sum\limits_{m=1,m\neq y_i}^C \Vert x_i-c_m \Vert) \tag{6}\]其中$G=3(C-1)(\frac{N}{C}-1)\frac{N}{C}$,很明显,$L_d(T,S)$是$L_t(T,S)$的一个上界,优化$L_d(T,S)$与优化$L_t(T,S)$在方向上是一致的。另外,观察式(6)可以发现,其物理意义就是缩小样本feature与所属类别类中心点的距离,同时扩大与其他类中心点的距离。
为了更严谨一些,我们还是要分析上界$L_d(T,S)$与$L_t(T,S)$到底相差多少?在满足什么条件的情况下,这个差异可以忽略不计?答案是centroid的选取要足够的均匀,centroids之间的最大与最小距离最好能保持一致。
论文当中给出了如下定理:
假定$\Vert x_i-c_{y_i}\Vert < \epsilon/2, \epsilon\geq0,1\leq i \leq N$,令$k_{min}=\min_{1\leq m,n\leq C,m\neq n}\Vert c_m-c_n \Vert$,$k_{max}=\max_{1\leq m,n\leq C,m\neq n} \Vert c_m-c_n\Vert$,则有$0\leq L_d(T,S)-L_t(T,S) \leq H(k_{max}-k_{min}+3\epsilon)$,其中$H=(\frac{N}{C}-1)N(N-\frac{N}{C})$为所有可能的三元组个数
具体的证明大家可以参考原论文,从定理中我们可以知道,$\epsilon$表示的是每个类的直径,而$k_{max}$与$k_{min}$是可以通过合理设置centroid控制的,理想情况下可以让二者相等。随着训练的进行,最终每个样本距离自己类别centroid的距离会越来越小,最终的$\epsilon$也会变的很小,此时$L_d(T,S)$就非常趋近于$L_t(T,S)$了
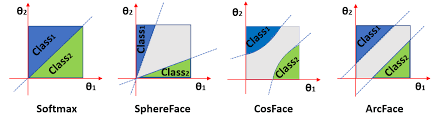
那么分析到这里我们可以先暂停一下,回忆一下人脸领域当中经常使用的ArcFace、CosFace或者SphereFace等系列方法。那么这些方法通常会对softmax输出进行一些调整,以达到缩小类内间距,增大类间间距的目的。
一般分类问题当中,我们有一个共识就是最后全连接层的权重$W$,其每一列实际上表示的是正是对应类别的类中心点,尤其是在上述魔改softmax下;对所有属于类别$c$的样本$\{x_i \mid y_i=c \}_{ i \in \{1,\cdots,N \}}$
需要满足$W_{c}x_{i}$最大,实际上就是要求二者夹角最小;
而对所有属于类别不属于$c$的样本$\{x_j \mid y_j \neq c\}_{j \in \{1,\cdots,N \}}$,
则需要满足$W_{c}x_{j}$尽可能小,也就是要求二者夹角尽可能大,至少要比$W_c$与$x_i$类内最大夹角要大。文字描述起来不太直观,直接上公式
\[\begin{align*} L_i &= -\log (\frac{e^{W_{y_i}x_i+b_{y_i}}}{\sum_je^{W_jx_i+b_j}}) \\ &=-\log (\frac{e^{\Vert W_{y_i}\Vert\Vert x_i\Vert\cos (\theta_{y_i},i)+b_{y_i}}}{\sum_j e^{\Vert W_j\Vert\Vert x_i\Vert\cos (\theta_j,i)+b_j}}) \end{align*} \tag{7}\]由于在魔改系列的softmax当中,一般都会提前进行norm操作,所以$\Vert W_i\Vert$和$\Vert x_i\Vert$的值均为1,偏置$b$在很多情况下也会被舍弃,所以我们唯一需要考虑的就是$\cos\theta$这一项,也就是要考虑样本和对应权重的夹角。观察分子和分母之间的关系,显然同类之间夹角越小($\cos\theta$越大),不同类之间夹角越大($\cos\theta$越小),分类的效果越好。然而普通的softmax这样分类就比较简单了,很容易收敛,得到的决策边界也就不是特别严格。所以为了提高分类效果,各种魔改softmax出现了,有的是把分子的$\cos\theta$变成$\cos m\theta$,有的是把$\cos\theta$变成$\cos\theta-m$,等等不一而足;总之无非就是想增加一下分类的难度,让决策边界变的更为紧凑。
最终能够满足条件的$W_c$其实也就是样本embedding集合$\{x_i \mid y_i=c\}_{i\in\{1,\cdots,N\}}$的类中心点了。
对比式(6)和式(7)我们发现,二者都涉及到了类中心centroid,只不过在triplet loss上界版中我们是显示的指定,而在softmax中是隐式的等同于权重$W$,差异无非是一个使用了余弦距离,而另外一个使用了欧式距离,实际上在做了归一化的情况下,余弦距离和欧式距离是等价的(只有系数上的差异)。所以总的来看,triplet loss与魔改softmax之间并没有什么本质上的区别。
但是从引入centroid这一点来看,我们还是能够得到不少启发的。在前面提到的论文当中,关于centroid的初始化,提到了两种策略:一种是one-hot centroids,另一种是K-means centroids,两者的目的都是为了保证类中心点足够的均匀,且相对距离相等。然而,反观FC层权重W的初始化,一般都是默认的随机初始化(可能会用xavier初始化或者kaiming初始化)。这种方式的缺点很明显,一旦重新训练,原来的embedding和新训练得到的embedding就相差甚远了,即使他们属于同一个类别。而采用可控的centroid初始化策略,不仅可以保证每次训练得到的embedding不会有太大变化,也便于未来对类别数量进行扩展(往里面加入新的centroid即可,其初始位置需要满足一定的距离约束),具体这样做行不行还需要进行实验验证。
0x02 从直观上说明为什么triplet loss不稳定
最后我们再来分析一下为什么单纯使用triplet loss效果不好,我们对比softmax的损失函数以及triplet loss上界版本的损失函数不难发现:softmax损失函数和triplet loss上界版本中,每一个batch的loss都能够兼顾全局的信息,并进行权重更新,这一点能够保证整个训练过程相对平滑稳定。其中softmax是天然如此,而triplet loss上界版则是通过引入centroid实现的。反观原始的triplet loss的形式,每个batch所涉及和更新的信息是非常局限的(只含2个类别),如果不能设计合理的采样和训练策略,很容易出现的一种情况是某个类别的embedding分布不稳定、出现突变和跃迁,导致训练反复、难以收敛。
这也正是为什么单纯用triplet loss进行训练难以收敛的原因,一般都会配上softmax loss一起训练。然而,从业内实践上来看,由于数据量的上升和各种魔改softmax的出现,我们目前在训练reid模型的时候,已经不使用triplet loss了。当然,鉴于目前深度学习属于一个“实验科学”的范畴,任何一刀切的说法都是比较naive的,triplet loss在数据量有限的场景下依然是有它的用武之地的;而数据量达到百万级以上(标签数在十万量级以上),那直接使用魔改softmax即可,收敛速度快效果又好,不用在triplet loss上苦苦调参了。
本文就是对triplet loss的一个小总结,及其与softmax等等之间的一些关联分析。如果我近期有时间做进一步的实验的话,再发出来供大家参考。最后还是要吹一波PyTorch,当初我们费了老大劲才写出来的triplet loss,现在PyTorch已经集成进去了TripletMarginLoss,又可以开心的当调包侠了呢~
如果觉得本文对您有帮助,欢迎打赏我一杯咖啡钱~

参考文献
- A Theoretically Sound Upper Bound on the Triplet Loss for Improving the Efficiency of Deep Distance Metric Learning
- Additive Margin Softmax for Face Verification
- 魔改softmax函数的决策边界
